secp256k1 vs. p256

Round 1!  (pun intended)

A recent conversation brought this snippet in:

...prime256v1 is not a widely used curve for altcoins and is regarded as very unsafe to use...

Every six months or so I return to this topic and repeat the research again, similar to the way I re-derive e.g. the quadratic equation and the chain rule every six months or so just to make sure nothing has changed.  So this time I figure I should document some of the discussion for future me and other researchers to speed the process along.

The issue is why Satoshi chose to use the elliptic curve known as secp256k1 as the basis for the elliptic curve digital signature algorithm (ECDSA) proving ownership of coin in BTC, and why I chose to use a different curve (prime256v1 aka X9_62_prime256v1 aka P256).  Satoshi's choice has been the source of endless speculation in various forums, and his stated reason "It was lying around" doesn't help much.

There is a broader discussion here of digital signature algorithms in general, and why ECC should be used over the easier-to-understand RSA.  As usual with cryptography, general distrust and unknown aspects of the discussion can lead one into a rabbit hole.  Personally I like the way ECDSA lets me easily verify the entropy on key generation:  It's a lot easier for me to pick a random number between 1 and 2^256 than it is for me to pick two random 256 bit primes.  Consider that the former can be done very quickly with dice and a pencil, no further hardware required.

But lets leave that discussion aside for now.  There are a few ways to evaluate this kind of thing.  The general problem is that one can only prove a cryptosystem is broken, not that it isn't.  There are a few ways however that we can have some good evidence that a cryptosystem isn't broken:

1.  --  Reputation - some people you trust say so
2.  --  Theory - logically it can be demonstrated to be at least as hard a something else
3.  --  Observation - a lot of people (including yourself) are using it to secure valuables which hackers want

If we are true scientists, with plenty of time on our hands, we ignore reputation almost entirely, only using it as a guide for what to consider first.  Double-blind peer review is the standard with which science would be best served.  But if reputation is your cup of tea, a decent review of these curves with an eye towards what various "authorities" have stated on the matter is here:

http://infosecurity.ch/20100926/not-every-elliptic-curve-is-the-same-trough-on-ecc-security/

The conclusion there is that the woodcoin curve X9_62_prime256v1 appears better than the bitcoin curve.  Well maybe.  There is also an inverse argument which suggests that what those authorities say should be taken as implicitly false (follow the white rabbit!).

As to the theory, sadly no proofs exist (even for RSA!), but there is plenty to read on the topic and it is well worthwhile to do so.

Let's go ahead and look at the curves themselves.  Both curves have the form:

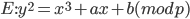
With a generator point (Gx, Gy), a prime order n, and an integer cofactor h.

I'll use a snippet from logaddress.org which shows all curve parameters for both curves:

ec.secNamedCurves = {
	// used by Bitcoin
	/*"secp256k1": function () {
		// p = 2^256 - 2^32 - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1
		var p = ec.fromHex("FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F");
		var a = BigInteger.ZERO;
		var b = ec.fromHex("7");
		var n = ec.fromHex("FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141");
		var h = BigInteger.ONE;
		var curve = new ec.CurveFp(p, a, b);
		var G = curve.decodePointHex("04"
				+ "79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798"
				+ "483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8");
		return new ec.X9Parameters(curve, G, n, h);
	}*/
	// used by Woodcoin
	"secp256v1": function () {
		// p = ???
		var p = ec.fromHex("FFFFFFFF00000001000000000000000000000000FFFFFFFFFFFFFFFFFFFFFFFF");
		var a = ec.fromHex("FFFFFFFF00000001000000000000000000000000FFFFFFFFFFFFFFFFFFFFFFFC");
		var b = ec.fromHex("5AC635D8AA3A93E7B3EBBD55769886BC651D06B0CC53B0F63BCE3C3E27D2604B");
		var n = ec.fromHex("FFFFFFFF00000000FFFFFFFFFFFFFFFFBCE6FAADA7179E84F3B9CAC2FC632551");
		var h = BigInteger.ONE;
		var curve = new ec.CurveFp(p, a, b);
		var G = curve.decodePointHex("04"
				+ "6B17D1F2E12C4247F8BCE6E563A440F277037D812DEB33A0F4A13945D898C296"
				+ "4FE342E2FE1A7F9B8EE7EB4A7C0F9E162BCE33576B315ECECBB6406837BF51F5");
		return new ec.X9Parameters(curve, G, n, h);
	}
};

The most obvious difference here is the a and b parameters.  The Koblitz curve has no linear paramater (a=0) and a constant parameter (b=7).  I personally have verified that this parameter is prime.  Compare this to the random parameter used in P256 (b=5AC635D8AA3A93E7B3EBBD55769886BC651D06B0CC53B0F63BCE3C3E27D2604B).  Which looks more secure upon first inspection?

This simplicity of a and b in secp256k1 leads to certain properties such as a faster-time signature verification and other tricks, but also leads to a faster Pollard's Rho algorithm to solve the discrete logarithm problem, that is to break the crypto.  Apparently it's not that much faster (less than a factor of 2 even), according to some authorities (unconfirmed by me).

which can be verified using some code I'm happy to share with you if you ask.

In theory it could be possible to pick exactly the right seed (SHA1 is to some extent broken after all) such that the resulting parameters yield a backdoored curve.  However, seeing as no method is known (to me at least) for making such a backdoored curve - even when picking parameters by hand (that isn't trivially noticed), this seems untenable.  At any rate, this kind of criticism can equally be applied to secp256k1.

Finally to the "observation".  What have we observed?  Personally I have not seen any of these curves broken.  Both are used to secure a large amount of assets of various types, but the very public nature of bitcoin (the 1st and by far largest public coin) leads one to believe that secp256k1 is now very well tested.

Conclusions?  There's sadly not much I can conclude from this.  If there were really serious doubts as to the usability and security of one set of elliptic curve parameters over another, we would use a script function which allowed a user to specify for a given TXO which curve would be used.  As it stands, other attacks are likely far easier at present, side channel, broken implementation, system level backdoors, and of course rubber hoses and red-hot pokers.  If you do have some reason to doubt secp256k1, even at some small percentage of your portfolio epsilon, you don't have much choice at the moment in public coins other than cryptonote or woodcoin.

Here's links to references I read in the last week or so on the topic, I'm not going to give you a formal list of references because I'm too lazy.  Mea culpa.

http://safecurves.cr.yp.to/complete.html

https://tools.ietf.org/html/draft-ietf-msec-mikey-ecc-03

https://perso.univ-rennes1.fr/sylvain.duquesne/master/standards/sec2_final.pdf

http://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.186-4.pdfo

http://www.secg.org/sec2-v2.pdf

http://research.microsoft.com/pubs/204914/734.pdf

http://eprint.iacr.org/2015/1018.pdf

https://cryptoexperts.github.io/million-dollar-curve/specifications/2016-02-01_trap-me-if-you-can.pdf