This post began with the title "Fiat economics". This however seemed like too much of an oxymoron to leave in place. "Fiat dynamics" was briefly the title as well. In the end, I went with Chumponomics. For relevant etymology you might want to read this.
Fiat dynamics is an odd subject to study in today's day and age (year 7, height 352k when this piece was started). It's a bit like returning to Ptolemaic astronomy. Indeed, why not place the Earth at the exact center of a set of large mechanical spheres which seem to move at arbitrary unexplained speeds? By setting the proper speeds and axes, one can in fact explain what one sees from the Earth. You don't agree? Imagine now that the source of your employment as an astronomer required you would take such an approach. In that case, this was the obvious way to approach astronomy. One could still make very important discoveries when phrased in the language of the celestial spheres. Some of the language (such as talk of declination and right ascension on the celestial sphere) survives to this day. Similarly, though better alternatives existed, many 20th century economists were paid in fiat currency of one sort or another. It makes sense they would phrase their economic discussion in the language demanded of them by their employers, despite its obvious shortcomings. Today fiat dynamics remains largely relevant in much of the world and historians and citizens will be picking up the pieces for a long time, so as you have already gathered, you are about to hear my take on it.
Economics (see Aristotle's "Oekonomikon") claims to be a scientific analysis of the management of the household. This includes all relevant incomes, expenditures, necessities and in more generality all goods and services which enter the household and are possible to be managed. The "household" can of course be taken in different ways, from one's immediate person to one's family home on up to entire continents or the whole spaceship or planet. Some of the factors involved in the household may have changed since the time of Aristotle (more energy resources, fewer slaves, for example) but the basic ideas are the same. Food, clothing, and shelter are common examples of immediately relevant resources in household management or economics. In so much as one would like to use precision and accuracy in describing relevant quantities to these important questions, one would like to use common units. Many fiat paid economists choose to use a fiat unit to describe economic quantities. However, this appears to be absurd to one familiar with the physical sciences. Imagine if you will:
Alice (about to mix something in a chemical beaker): How many grams again is the mass of 1 cubic centimeter of water at standard temperature and pressure (STP)?
Bob: Well we are given the figure of 2.15 by National institute of standards and technology (NIST) but ShadowUnits assures us it is more like 3 or 3 and a half.
Alice: We'd better wait for the official announcement from the NIST spokesman this month. If they delay on the increase in grams per liter another month we will have to adjust these numbers down for our Nature publication this summer.
Bob: Don't worry, we factored that into our budget after they upped Avagadro's number in China last year.
As you can tell, a fiat unit such as the US dollar is not a unit a reasonable person would use to describe any kind of quantity of long term importance, simply because we don't now how much of it will be around after a long time (in fact we don't know how much is around now either). It is a unit devoid of physical definition. It is now becoming clear to a majority of 21st century literates that any discussion of relevant economic quantities of importance (such as revenues, net worth, inherent value, prosperity, or any cost benefit analysis) which reports numbers in fiat units such as the US dollar is completely laughable. It is chumponomics. The reporting of relevant figures in fiat units is only done to satisfy wealthy benefactors or to continue in profiting from errors of the chumps who might believe this shite.
That being said, the question of how much fiat people do have now, and how they get it, is the heart of chumponomics. A pair of US dollars can be seen as what lies between you and a hotel room for a night in coastal Ecuador, or ten thousand dollars can be seen as what lies between you and a hotel room for a night in a certain resort on Mykanos. Let's just continue onwards into this realm and leave behind the ideas of household management (food, clothing, shelter, sustainable agriculture, not killing yourself, etc). Those are indeed important things (and depending on the misfortune of your current situation they may seem to depend on chumponomics) but I'm not really going to get into them now. Let's talk fiat.
Towards a theory of chumponomics
Point of fact: chumponomics is the study of one phenomenon (and its subsidiary effects). This phenomenon can be referred to as "inflation". The proof of this is quite simple. All fiat is produced by inflation, that is, inflation of the money supply at effectively zero cost (or at least great discount) to those inflating it. The origin of every dollar, every yuan, every euro, was that it was created out of nothing by fiat. Thus, if we study fiat dynamics, we have as our primary function to study inflation.
Let's consider two extreme examples to begin this discussion. One I will call "perfectly balanced inflation" and the other "perfectly imbalanced inflation". In perfectly balanced inflation, the increase of the money supply proceeds exactly as a stock split. Every owner of a unit of the corporate scrip becomes the owner of two units (the exact factor is unimportant). The result is that most users of the fiat are aware immediately of the new distribution. Prices immediately go up accordingly. There is no change to the distribution of relative ownership of the total supply, but gross domestic product (GDP) has doubled. This assumes only that one is calculating GDP in the fiat unit, not how it precisely was counted.
In the second example, we again double the money supply, but in this case give all the new scrip to one person, let's call him the king. The king being a miser, puts it all in a warehouse and spends not a penny. In this case we have doubled the money supply but the prices stay the same and the GDP is unchanged. This is an unstable arrangement. At some point, the king might be tempted to reach into the warehouse. Some employees might sneak a wheelbarrow full from the warehouse. Eventually, the stuff will start to leak out. More likely, when word gets out what will happen is the king will face insurrection. Perhaps the warehouse will be looted. This kind of arrangement is unstable because to maintain such a position one needs pay off a group of colleagues with a portion of the proceeds in order to keep them as guards for the operation. As you can clearly tell, this is much closer to the way things were run in the fiat era.
The physicist might see at this point that what we are talking about is a diffusive process. The pile of new fiat is like a lump of salt in a glass of water. In the case of the water it is the motion of heat in the water and collisional and chemical effects that start to erode at the salt and begin the distribution and smooth the salinity gradient. For the case of perfectly balanced inflation, we will have a solution of doubled local salinity throughout. In case you hadn't noticed, chumpanomics involves continued inflation and so the system is sometimes referred to as "disequilibrium".
One could study chumpotronic diffusion as one studied spatial diffusion, and calculate for example the spatial density of fiat on the Earth's surface. It is clear from the air that there are places where the fiat is introduced, such as London, Washington DC, and Beijing, with a higher density. Construction projects and so-called development projects, regardless of their true economic impact (which is often negative) can be point sources of fiat inflation. Other places await for diffusion to slowly reach them via trade. However, calculating the relevant spatial diffusion coefficients is difficult. The physical barriers to motion of a unit of fiat currency are not the same as those that control the movement of a salt ion. While there are some barriers to physical motion, fiat can in fact jump across the globe. We might therefore also be interested in an adapted theory of diffusion, not in spatial dimension but in a larger dimensional space of participants.
Fiat Diffusion
Consider the discrete fiat density vector 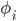 , which describes the amount of fiat controlled by the ith participant from a group of n total participants. We can describe the evolution of this quantity with time t, first by producing a continuity equation:
, which describes the amount of fiat controlled by the ith participant from a group of n total participants. We can describe the evolution of this quantity with time t, first by producing a continuity equation:
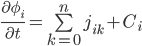 Eq. 1
Eq. 1
Here we have introduced a flux term 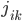 describing the flux of fiat from the kth participant to the ith participant, and a counterfeiting source term
describing the flux of fiat from the kth participant to the ith participant, and a counterfeiting source term 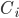 describing the amount of new fiat created (or destroyed) by the ith participant. Note that for the purposes of describing fiat dynamics it matters not at all whether the inflationary source
describing the amount of new fiat created (or destroyed) by the ith participant. Note that for the purposes of describing fiat dynamics it matters not at all whether the inflationary source 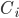 is licensed or described as issuance as opposed to criminal counterfeiting. The result is the same to the participants as long as it remains a source (or sink). To proceed we need to describe the flux term, which we can approximate as being to first order proportional to the difference in fiat holdings between the two participants:
is licensed or described as issuance as opposed to criminal counterfeiting. The result is the same to the participants as long as it remains a source (or sink). To proceed we need to describe the flux term, which we can approximate as being to first order proportional to the difference in fiat holdings between the two participants:
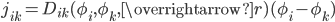 Eq. 2
Eq. 2
In other words, we expect fiat rich people to buy things from fiat poor people, on average, and the rate of this flow is to first order proportional to the difference in their relative holdings. Here we have introduced a set of diffusion coefficients 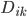 which depend on the relative levels of fiat held by the ith and kth participant as well as external variables which we have lumped into the vector
which depend on the relative levels of fiat held by the ith and kth participant as well as external variables which we have lumped into the vector 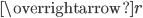 . We can produce now a canonical diffusion equation for chumponomics:
. We can produce now a canonical diffusion equation for chumponomics:
 Eq. 3
Eq. 3
What next?
At this point it is tempting to go into which external variables affect the diffusion coefficients and to state this explicitly. Language barriers, trade practices, and of course geographic location will all play a role in the vector 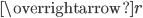 of external variables. Also, second order effects will emerge in which the relative flow is not a linear function of the difference in holdings between participants. It is for this reason that we have explicit dependance of the diffusion coefficients on the actual amount of fiat held by the two participants for each coefficient
of external variables. Also, second order effects will emerge in which the relative flow is not a linear function of the difference in holdings between participants. It is for this reason that we have explicit dependance of the diffusion coefficients on the actual amount of fiat held by the two participants for each coefficient 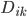 . However, to what end? It is clear immediately upon inspection that an understanding of these diffusion coefficients, which could in theory explain the whole of economic interaction, is not going to allow us to calculate diddly squat. Why? Because we have no idea what the counterfeiting terms
. However, to what end? It is clear immediately upon inspection that an understanding of these diffusion coefficients, which could in theory explain the whole of economic interaction, is not going to allow us to calculate diddly squat. Why? Because we have no idea what the counterfeiting terms 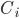 are doing.
are doing.
Imagine that you are a chemist told to use the diffusion equation to calculate salinity in a large body of water. After writing down the relevant diffusion equation, you are then told that by the way salt is being added in unknown places at unknown quantities. Does this seem like a useful exercise to you? No. The only way to do well is to somehow learn what one can about the sources of salt, perhaps by paying off the salt delivery guy. Bothering with molecular dynamics, heat, and convection, will be a waste of time. This is the attitude of the seasoned chumponomist: Who cares about efficiency, velocity of money, real revenues or productivity? What matters is who you know, and how close they are to the sources.
Fiat monetary systems are only useful as chumpotrons, that is, as scams. In terms of the global economy, or the survival of humanity and Gaia, they are a massive cement weights attached to the legs of humanity. The only questions emerging for the educated 21st century economist are what pieces of the formalism of 20th chumponomics can survive into the 21st century and still be useful. My guess is many. Language is phenomenally adaptive. Already we are using words like "accounts", "wallets", "interest", and "market capitalization" which had fiat significance, to mean slightly different things in the world of monetary systems which have public and deterministic 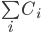 . Other than that, don't waste your time with chumponomics.
. Other than that, don't waste your time with chumponomics.
2 Replies to “On Chumponomics”