Equality

Lets open this up with a quote:

“If you have something to say, write an equation.  If you don’t have anything to say, write an essay”.  — Paul Erdös

You see, we need equality to write an equation.  We need the notion of equality to conceive of a tonal world, a world which symbols can describe.  It turns out the “real world” is not tonal.  Symbols never give you precise reality; the map is not the territory.  However, seeing as you are “reading” at this very moment, and things seem to at least partially be “working”, lets continue.  Why not?  Communication, though imperfect (see Shannon for details), is something worth doing.  To do so requires equality – on many levels.  In fact, we can phrase a stronger statement:

For all objects A and B chosen from any sets S_A and S_B, there exists an infinite set of functions f_i such that:

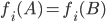
Or more simply put:  all things are equal, for an infinite number of metrics.  To not see a myriad of ways that any object is equal to another is to simply have a broken imagination.  How is 100 like 1?  How is the sun like an electron?  How is an apple like another apple, or like a racecar?  It’s called thinking.

Now that we have established that all things are equal (and that it’s possible to think) lets look at the converse: all things are unequal.

For all objects A and B chosen from any sets S_A and S_B, an infinite set of functions g_i exist such that:

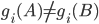
This seems obvious, but consider the case when A and B are the same object.  Does such a function exist?  In fact it does.  Is it possible that:

?

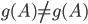Well yes.  The A on the left is “on the left” whereas the A on the right is “on the right”.  Is that enough?  Also there exist functions such as:

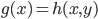
where y increments upon every evaluation of h. For such functions, we can easily construct an h and g such that :

g(0)==g(0)

is false.

So lets review.  All objects have equality under some metrics.  No objects have equality under all metrics.

Now go write some equations.