If you've been following the rise of public coins, you have probably heard the term "premine". In a public coin, the money supply is public - thus anyone can see when and how all the money was created. Traditionally, if monetary tokens were distributed before the transactions began on the network, before the transaction validation known as mining began, this was referred to as a premine. Coinmarketcap.com for example allows you to filter out premined coins from their list. But what is their criteria for a premine?
Well it's easy to look at the code some nodes are running and see a hardcoded distribution before mining began. Coins like ethereum, nxt, and plenty of others obviously have a premine in the code, while BTC, LOG, LTC, DOGE and yes even BCN do not. However, this is not the whole story.
As more and more public coins were released, their creators used different methods to keep certain portions of the currency for themselves. Some of these were referred to as a "ninja mine". In this case rather than code a premine into the blockchain definition, they would simply mine the first blocks themselves before publicizing the existence of the coin.
And why not play these games? There's no reason a priori why a premine or a ninja mine is fraudulent. After all, the money supply is public. If people still want to use the coin, then they are at least doing so with the knowledge available to them (unlike e.g. a fiat currency in which there is no way to verify anything about how many tokens have been issued on a given day). There are many reasons given by various coin proponents that a premine is a positive thing, such as to fund development related to the coin, or to fund an ICO for an initial distribution. However, an individual wishing to decide which coin to use might be interested in just how premined a coin is. Well, how premined is your money?
There are two areas of potential interest here addressing the premine, one is how much money was premined, that is how much existed prior to a given moment in time - and the other is who got it. For the purposes of this post, I will ignore the latter. In other words, we will assume that if somebody who isn't you got the money, than it's part of the premine. Sure, you'd rather Alice (and her friends) had it rather than Bob, but lets assume for now that this is a separate issue.
Quantifying premine via a scalar quantity is in fact not necessarily the right thing to do. The proper way to look at a coin's distribution is to look at the entire money supply curve vs. time. Some distribution curves seem fair early on and become more front-heavy later. Others might start out ninja-mined but look more fair later. But hey, we want numbers, and now! So lets pick some parameters.
The simplest way to do it is to pick a time interval, and look at the endpoints. In other words, we are going to compare two points on the money supply curve: one at some time, such as the present, and another in the future. The method is very simple:
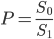
where P is our scalar index of premine, 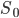 is the money supply at some time T_0, and
is the money supply at some time T_0, and 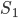 is the money supply at some future time T_1.
is the money supply at some future time T_1.
Okay! So, now for some numbers.
| COIN | P0_1 | P0_10 | P0_30 | P10_30 | P30_100 |
| BTC | 0.96 | 0.79 | 0.76 | 0.96 | 0.995 |
| LTC | 0.90 | 0.61 | 0.65 | 0.92 | 0.994 |
| LOG | 0.93 | 0.78 | 0.71 | 0.906 | 0.902 |
| ETH/ETC | 0.89 | 0.44 | 0.21 | 0.47 | 0.35 |
| DOGE | 0.95 | 0.47 | 0.40 | 0.60 | 0.42 |
| NXT/RIPPLE | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
Here we have calculated a premine factor for five different choices of the time interval. The first three begin with the present time and extend to one, ten, and thirty years in the future. The next is the premine factor which one would find ten years from now, comparing to thirty years from now. The final factor is what one would find in thirty years, comparing to a hundred years from now.
The first thing we notice is that premine factors for coins like NXT and RIPPLE don't change regardless of the interval in consideration. They remain fully premined. One advantage of such a monetary supply curve is that there is never any supply inflation. However, there is also no incentive for new miners to come in and secure the network. This means there is also a disadvantage due to resulting centralization.
Another thing to note is that even though ETH/ETC has a hardcoded premine, it doesn't look so bad with our premine metric. Why is that? The reason is the infinite inflation schedule, with a fixed reward per block, just like DOGE. In fact our shortest interval premine factor shows ETH/ETC as the least premined coin. This looks good according to our metric, as we see that the premine factor for these coins is quite low, even in the longer time intervals. However, the disadvantage is that there is no cap on the supply and a continual supply inflation. This makes an effective demmurage and so long-term investors will be unlikely to hold these coins.
The difference seen between BTC and LTC is solely due to the delayed launch of LTC, as these coins share the same supply curve characteristics apart from a factor of four in absolute size. As we consider later time periods, this phase shift makes less and less of a difference.
The first three coins in the table have a capped supply, and so the premine factor must always increase. Other coins like DASH and XMR also share this basic pattern, and show a similar P_30_100. However, the logarithmic supply curve shows its advantage quite nicely in this metric. Even though the supply is capped and the inflation remains limited, there remains a far greater amount of coinbase to give out to future miners.
Coins like BTC, LTC, XMR and DASH will in another decade or three remain secure and decentralized only if transaction fees are large enough to incentivize miners, due to their coinbase reward dropping exponentially with time. However coins with a logarithmic supply curve do not have an exponential reward drop but an inverse function. This allows them to maintain long-term inflation free behavior without hitting an asymptotic wall of TX fee dependence.
1 Reply to “Addressing the premine”