“The Majority is Enough”

Abstract:

About a year after Ittay Eyal published two papers claiming vulnerabilities in the bitcoin mining protocol, we have seen that the network is still strong (it has grown in hashpower many times over) and is unaffected by the supposed problems. I show here the biggest reasons the two vulnerability analyses were flawed. The attacks appear to hinder other miners who are competitors. However, both of the attacks harm the attacker's bottom line more than any harm to the competitors can emerge as profits for the attacker.

Selfish Mining Attack

This is discussed in [Eyal and Sirer, 2013]. The attack suggested is to not publish solved blocks immediately, working on their successors in private. The idea is that the attacker can work on finding another block to build off their private unpublished chain, while other miners are doing work that could be proven stale were the attacker to find yet another block. However, more often somebody else will first find a block that competes with the original one found and kept private by the attacker. The authors address this as follows:

“In the first scenario where the honest nodes succeed in finding a block on the public branch, nullifying the selfish pool's lead, the pool immediately publishes its private branch (of length one). This yields a toss-up where either branch may win.”

In fact if an attacker waits until he sees another block on the network, the attacker can be sure that a majority of hashpower is now working on successors to that already published block, and not the one the attacker has kept hidden. The result is not a toss-up, but a distinct advantage to the honest nodes who have published their blocks already. This first order error in the resulting analysis of reward is larger than all the other effects considered in the paper. A fast connection to the network and publishing blocks immediately after they are found is of utmost importance in efficient pool operation. The proposed “selfish miner” is throwing away some percentage of his reward for the privilege of winning a much smaller percentage back.

The Miners Dilemma

In this paper [Eyal, 2014] we see a supposed game theory analysis of bitcoin mining with the option of a “block withholding attack” which is referred to as “infiltration”. This attack is one in which a pool operator sends some of his hashpower to another pool, submitting shares of work, but discarding any work which finds valid blocks.

The game theory analysis is flawed in a few ways, one of which being that it is confused as to who the players of the game are. It mostly appears to be the pool operators are the game participants but at times it seems to be the individual miners. The biggest problem is however seen in this quote:

“The attacker’s mining power is reduced, since some of its miners are used for block withholding, but it earns additional revenue through its infiltration of the other pool.”

In fact we can see intuitively that there is no additional revenue through infiltration of another pool. This so called infiltration consists entirely of throwing away money (solved blocks), which hardly can be considered “additional revenue”.

The mathematics begins well enough, as the author presents a case of one pool infiltrating another with some amount x of hashpower in Equation 5. However something clearly has gone wrong when they give us the revenue per miner of attacking pool r₁ in the expression below equation 7. Here setting the infiltration rate x to 0 gives us r₁=1, rather than something proportional to m₁. Dimensional analysis also shows something is wrong with the expression given, and the resulting conclusions such as in e.g. equation 8 do not make sense under dimensional analysis. The correct expression for the revenue of the attacking pool is:

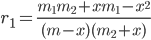                        Eq. 1

Here r₁ is the total revenue of pool 1. We can see that if x goes to zero, r₁ goes to m₁/m as it should, because the revenue is expressed as a fraction of the total network coinbase rewards. A linearization of the expression in the limit of small x (ignoring x² terms) gives us

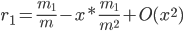                 Eq. 2

This shows that a small increase in infiltration of another pool leads to a small loss of revenue. This is a traditional Nash equilibrium at x=0, exactly contrary to the conclusions of the quoted paper.

The situation for two pools which both can both use infiltration is somewhat more complex symbolically. Equation 11 in the paper appears sound. However we can see the same equilibrium will be reached in this case, as clearly one pool throwing money away does not lead to incentive for another to throw money away. The equilibrium game theory solution is that neither pool infiltrates the other. Real world behavior of miners supports this conclusion.

The situation is more clear when considering a miner who is infiltrating a victim pool. When a solved block is found, this miner could receive a fraction of the block's coinbase from the pool by submitting it. However, the miner does not submit the block. Without further context this action could only be irrational and the equations 1 and 2 show the amount of loss expected for the attacker.

Discussion

The operation and theory behind bitcoin mining operations is certainly worthy of discussion and there are many potential viable attacks such as DDOS of competing pools, collusion to obtain large percentage of hashrate, and considerations of rapidly moving miners which all could lead to interesting game theory analysis. The speed in which miners can move, the payout schemes implemented, and the relative transparency as well as transaction acceptance are all relevant here. However, the strategies considered by the authors in these two papers are not vulnerabilities.

Acknowledgements

Helpful discussion in the #bitcoin-assets freenode IRC forum are acknowledged. This work is not supported by any governmental or grant. Contributions are graciously accepted at the following address: 1Jj5bzgb5wCc69Rtemm43QyGxEmaDL9LEN.

References

arXiv:1411.7099

arXiv:1311.0243